Muitos de nós observamos uma forte ligação entre a matemática e a arte, mas a relação entre as duas áreas pode ser muito mais profunda do que normalmente se supõe. A ligação entre a criação artística e a matemática não se limita à ciência de desenhar em perspectiva ou às deslumbrantes tesselações do artista gráfico M. C. Escher. Assim como a própria pintura, a matemática é um processo criativo e uma busca da simetria e da beleza.
Nos últimos cinco anos, estive envolvida num projeto intitulado “Mod Art”. Embora este trabalho seja dedicado especificamente à transformação da aritmética modular em desenhos artísticos, acredito que a mod art proporciona uma lição fundamental sobre os valores estéticos semelhantes da matemática e da arte. Mostrar exatamente como um padrão de mod art é criado também revela parte da rica interação que existe entre as duas áreas.
Na verdade, a aritmética modular é um conceito com o qual todos estamos bastante familiarizados. Por exemplo, se um relógio analógico indicar que são dez horas, três horas mais tarde será uma hora (e não treze, que seria o resultado de uma adição simples). A aritmética modular é nada mais do que uma versão ‘mais interessante’ da aritmética do relógio, sendo também uma técnica inestimável para os matemáticos que estudam a teoria dos números.
Por uma questão de rigor, usamos o termo inteiros módulo n que definimos como o conjunto finito {0, 1, 2, …, n-1}, juntamente com uma adição e uma multiplicação que atuam sobre esse conjunto. Estas operações diferem das comuns porque, após obtermos o resultado ‘convencional’, subtraímos repetidamente o módulo n do resultado até que este fique entre 0 e n-1. Este processo equivale a dividir a resposta pelo módulo e manter apenas o resto dessa divisão.
Por exemplo, os inteiros módulo 4 são o conjunto {0, 1, 2, 3} com as tabelas completas de adição e multiplicação apresentadas desta forma:
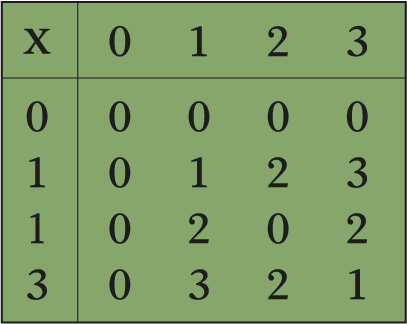
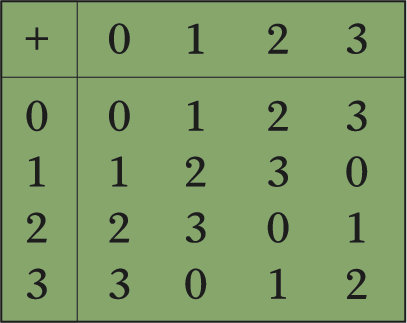
Observe que 1 + 2 ≡ 3 (mod 4), uma vez que 3 está entre 0 e 4 – 1 = 3, e 3 × 3 = 9 ≡ 1 (mod 4), já que 9 dividido por 4 tem resto de 1. As três barras horizontais (≡) indicam uma relação de congruência em vez de uma equivalência comum.
Para continuar a leitura, basta visitar e fazer o download clicando aqui.
